最近遇到很头疼的一件事，比较2个浮点数的大小，可能想想应该很简单。不就一行代码的事吗？但是也就是因为一行代码引发了不可想象的后果。

证券业务中会有新股认购这个模块，提供给客户进行认购即将上市的股票。新股认购中最主要的普通认购分为现金认购和融资认购。遇到的问题就出在融资认购上。

融资认购的意思就是：认购股票总金额 = 一部分现金 + 一部分融资（说白了就是贷款）。

来看问题：

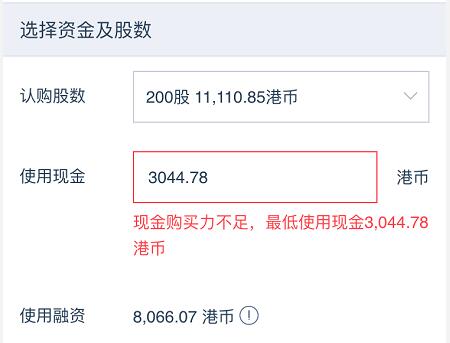
上面本来融资认购200股股票总金额为11110.85港币，其中使用现金3044.78港币，使用融资8066.07港币。

正常情况应该是正确的。但是程序却提示购买力不足。这就有问题了。

并不是说上面的3个数相减不相等，而是可能是背后的其它浮点数计算逻辑导致。

这问题背后的根源就是JavaScript浮点数相减。

实际的开发中，难免会进行浮点数进行计算和判断大小。然后通过条件if语句执行相关的操作。

举个栗子，一个简单的比较2个浮点数的大小：

function testAB(){
  let a = 34.16;
  let b = 34.16;

  if( a === b ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

上面的一直会执行if语句里面的console，输出a === b，这是确信无疑的。

那下面这个，还能拍着胸脯说是相等的吗？

function testAB(){
  let a = 34.17;
  let b = 34.16;

  if( (a - 0.01) === b ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

答案很显然，这里会输出a !== b。

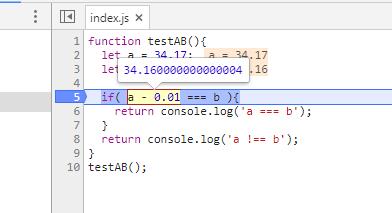
为什么 34.17-0.01 !== 34.16？

有时候就是这样，所想的和真正看到的完全是不一样的。难道JavaScript的数学是体育老师教的吗？然而并不是。

问题还得从JavaScript语言本身找：

• 第一，因为十进制浮点数在计算的时候都会被转换成二进制，但由于浮点数用二进制表达时是无穷的。所以2个无穷的数相加，得到的数也是无穷的。
• 第二，IEEE 754标准的64位双精度浮点数的小数部分最多支持53位二进制位。意味着2个浮点数相加的结果只会保留53位二进制位，53位后面的都会被切掉。

由于上面的2个原因，最终导致计算出来的结果被转换成十进制数的时候，其实是一个近似值（因为浮点数二进制53位以后的部分都被切掉了）。

所以：

34.17 - 0.01 !== 34.16;
0.1 + 0.2 !== 0.3;

详细解释可查看 这篇文章。

解决浮点数问题

问题知道了，现在要做的是正确的解决问题。

首先想到的是将计算逻辑移到if语句之外，这看起里会和第一个正确的比较很类似。

function testAB(){
  let a = 34.17;
  a = a - 0.01;
  let b = 34.16;

  if( a === b ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

现实是残酷的，这是行不通的。这只能证明一点，精度的计算和位置无关。也就是说，与a - 0.01 表达式放置的位置无关。

【方案1】toFixed方法

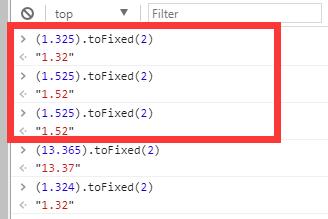
这里考虑到只保留2位小数。所以使用toFixed(2)方法，该方法在必要时会进行四舍六入，然后转成字符串。调用完toFixed方法后，最后再将字符串转为Number类型（JavaScript里面浮点数也算Number类型）再比较。

注意：这里发现toFixed并不一定都会四舍五入。

function testAB(){
  let a = 34.17;
  a = a - 0.01;
  let b = 34.16;

  if( +(a.toFixed(2)) === b ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

这确实得到了一正确结果。但是，说实话我对使用toFixed这个并不赞同。

发现 toFixed 的一个相乘问题

背景是这样的，一般数据库不会保存浮点数，都会把浮点数转换成整数保存。

例如这个价格200.67这个值，可能数据库会保存为200670（即：200.67 * 1000）。

现在按上面的toFixed(2)方法取两位小数然后*1000进行保存，会得到正确的结果200670。

let price = 200.67;
price = +(price.toFixed(2)) * 1000;

console.log(price); //输出：200670

但是，凡是总有例外。下面是一段代码里面按上面的方法计算stockPrice之后，乘以1000。得出来的结果。

发现股数6000时，股价居然为32908309.999999996（其实正确的值应该为32908310，不应该存在小数位才对）。

也就是因为这一个数字，导致客户在认购6000股的时候，认购失败。

结论：使用toFixed方法处理之后的数字乘以某个数，计算出来的值有可能还是会存在小数。

【方案二】 尝试使用Number.EPSILON

表示1和大于1的最小值（可表示为 Number）的差值。Number.EPSILON实际上是JavaScript能够表示的最小精度。误差如果小于这个值，就可以认为已经没有意义了，即不存在误差了。

这里 Number.EPSILON = 2.220446049250313e-16

function testAB(){
  let a = 34.17;
  let b = 34.16;

  if( a - 0.01 - b < Number.EPSILON ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

发现输出的是a !=== b。不甘心调换位置试试。

function testAB(){
  let a = 34.17;
  let b = 34.16;

  if( b - (a - 0.01) < Number.EPSILON ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

发现输出a === b。两种截然不同的结果。

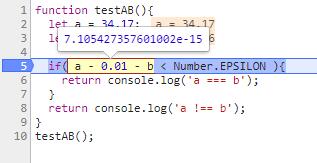
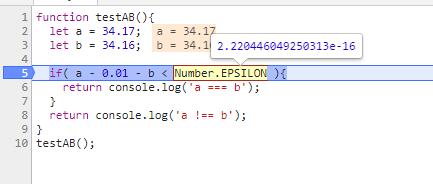
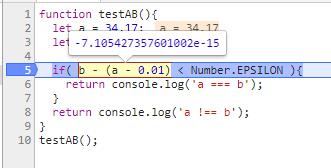
结果1：7.105427357601002e-15 大于 2.220446049250313e-16。输出a !== b。 结果2：-7.105427357601002e-15 小于 2.220446049250313e-16。输出a === b。

使用Math.abs取整进行比较:

function testAB(){
  let a = 34.17;
  let b = 34.16;

  if( Math.abs(a - 0.01 - b) < Number.EPSILON ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

依然输出a !== b。由此得出不能使用Number.EPSILON。

【方案三】Math.round函数

这个方法是会对浮点数进行四舍五入，保存为整数进行比较。对于保留2位小数的浮点数。只需要*100然后取整比较就可以。

function testAB(){
  let a = 34.17;
  a = a - 0.01;
  let b = 34.16;

  if( Math.round(a * 100)  === Math.round(b * 100) ){
    return console.log('a === b');
  }
  return console.log('a !== b');
}
testAB();

依此类推，3位小数的可以*1000。

推荐使用Math.round。

总结

切莫眼高手低，马失前蹄。

作者：Jin